Les collections de Jean-Marie

Les Bâtons de NEPER
et réglettes de GENAILLE

NEPER

Dispositif de calcul inventé en 1617
John Napier, dit NEPER était un savant écossais du XVIe siècle, né à Merchiston en 1550.

Théologien, astronome et également physicien et mathématicien, il inventa les logarithmes pour simplifier les calculs astronomiques.
Et pour simplifier les multiplications il créa le procédé dit "Bâtons de Neper".

A l’aide de ces bâtons il est possible de multiplier des nombres même sans savoir la table de multiplication.
Sur ces petits bâtons carrés sont mentionnés sur chacune des faces les multiples d'un chiffre (1 à 9).
En disposant, sur un petit plateau joint, les bâtons correspondants aux chiffres du multiplicande, et en notant la disposition obtenue en face des chiffres du multiplicateur (chiffres du plateau), quelques additions simples permettent d'obtenir le résultat d'une multiplication importante :

Exemple d’utilisation :
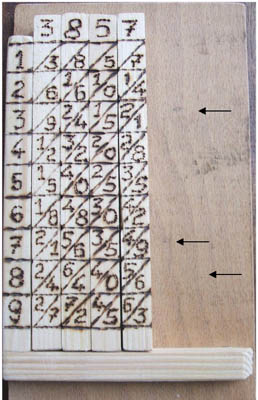
Pour multiplier 3857 par 738
Il suffit de placer côte à côte les batons intitulés 3 , 8 , 5 , 7 .
et de recopier les lignes sur un papier, puis d'additionner les différentes colonnes diagonales en commençant par la droite,
en tenant compte des retenues , ce qui revient à des additions de chiffres simples pour obtenir le résultat.

Ce système fut utilisé avec beaucoup de succès dans toute l’Europe aux XVIIe, XVIIIe et XIXe siècles.


Mode d'emploi des "Bâtons de Neper" (PDF)

En imprimant recto (et verso) sur un bristol A4 (ou sur une feuille collée ensuite sur un carton) les 2 pages ci_dessous, vous pouvez créer un ensemble simplifié de Bâtons de Neper :
"Bâtons de Neper" recto(PDF)
"Bâtons de Neper" verso(PDF)
Et, lors de l'impression, en modifiant l'échelle du document en fonction de la largeur de baguettes carrées, un peu de colle permet de créer de véritables Bâtons de Neper: après avoir imprimé plusieurs 'recto', il suffit de laisser les bandes groupées par quatre, en variant les groupes, et de plier sur les traits oranges intermédiaires.

                               
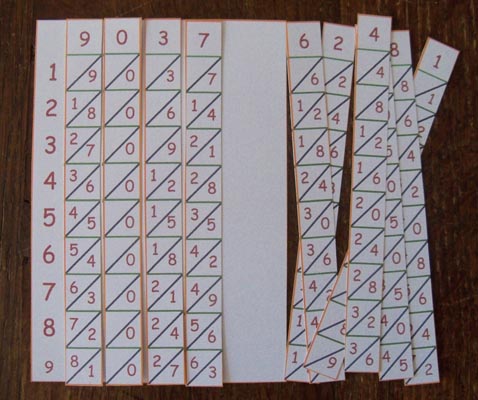
                     Bâtons de Neper simplifiés en bristol,                                                              et Bâtons de Neper sur bois carré

GENAILLE

Henri GENAILLE ingénieur d'armement et/ou ingénieur des chemins de fer de l'état (selon les sources) a créé en 1885 cette simplification des bâtons de Neper.
Chaque réglette, dispose de 8 cases ( correspondant aux lignes 2 à 9) sur lesquelles on trouve à droite une suite de chiffres s'incrémentant de 1 vers le bas, et à leur gauche 1 ou 2 triangles désignant le chiffre de la réglette de gauche à utiliser (automatiquement en fonction de la retenue).


Mode d'emploi des "Réglettes de Genaille" (PDF)


Comme pour les bâtons de Neper, vous pouvez imprimer sur bristol et créer des réglettes de Genaille :

Réglettes de Genaille (PDF)

Et les couper séparémént ou par quatre collées ensuite sur baguettes bois.